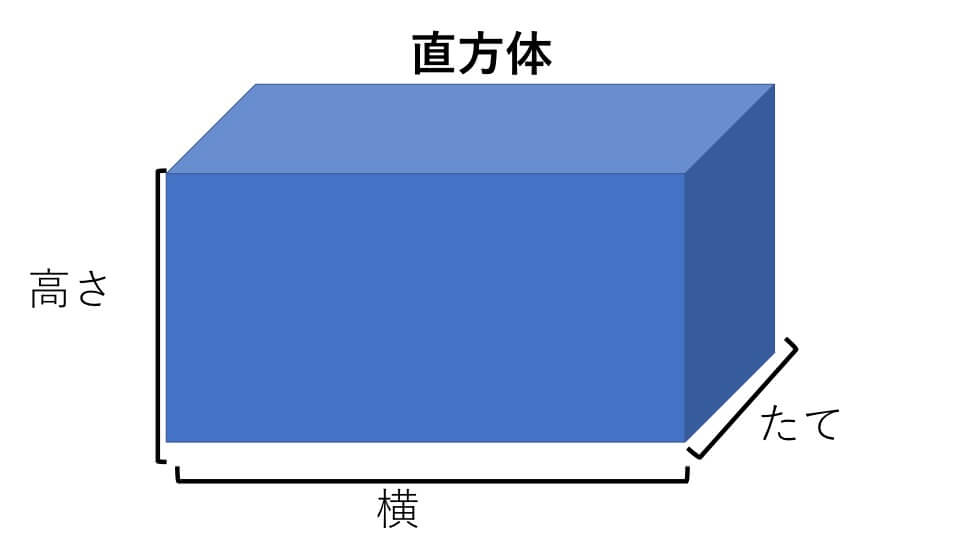
直方体の体積の求め方から,四角柱の求 積公式を考えている。 関・意・態(ノート,発言) 四角柱の体積の求め方から,三角柱 やいろいろな角柱の体積を求めることが できる。 考( ノート) 円柱の体積も,底面積×高さで求められ6年算数 立体の体積 その1 子どもの学習支援 by いっちに算数 スマホ版 立方体 直方体 6年生は、上の図のように5年生で勉強した「直方体や立方体」の体積の求め方を生かして、下の図のような「三角柱などの角柱や円柱」の体積の求め方を勉強します。イ 立方体及び直方体の体積の求め方を考えること。 量と測定においては、長さやかさ(体積)について第2学年で、㎝やm、dlやLといった単位の大き さを基に測定する活動を通して、長さやかさの概念、それぞれの単位の相互関係を学習している。第4
直方体の表面積の求め方は 1分でわかる計算 公式と例題
直方体 体積 求め方
直方体 体積 求め方-(例)横に補助線を2本引くと, 直方体Aは18×(50-25-15)×(40-10-) 直方体Bは18×(50-15)× 10 直方体Cは18×50× になります。3つの直方体を足すと,全体の体積が求められます。 ( cm3 )(技能) ・直方体,立方体の体積を,公式を用いて求めることができる。 (知識・理解) ・体積について,単位と測定の意味や,直方体や立方体の体積は計算によって求められることやその求め方 を理解し,体積の量感を身につける。




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習
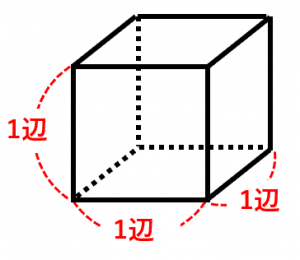
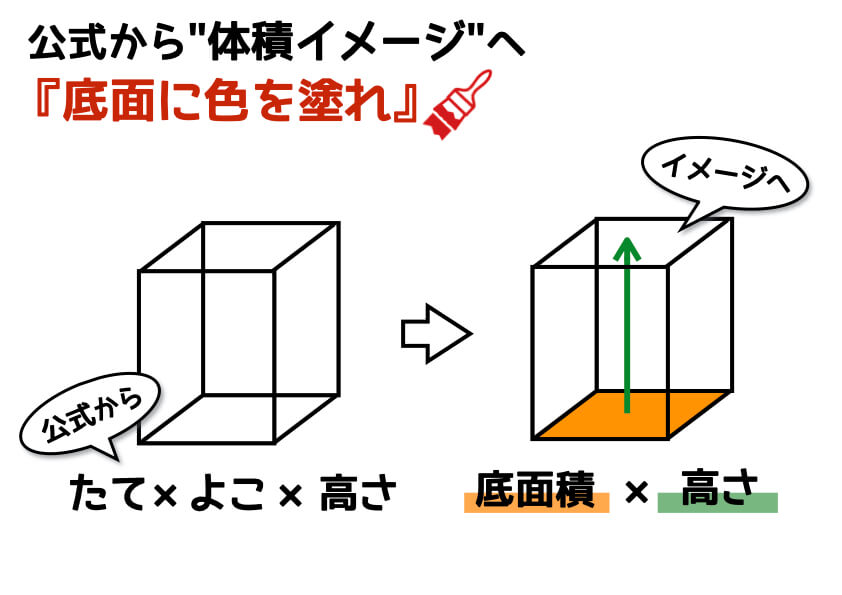
全体の直方体から、くりぬいてある部分の体積を差し引きます。 $$4\times 6\times 5 3\times 2\times 5=90$$求める立体の体積は\ (90cm^3\)となります。 2の解説 計算の手間から考えると、2つの直方体に分けて考えるとやりやすいと思います。 今回は、立方体と直方体の体積の求め方(公式)について書いていきたいと思います。 立方体の体積の求め方公式 直方体の体積の求め方公式 立方体・直方体の体積を求める問題 問題① 《立方体の体積の求め方》 問題② 《立方体の体積の求め方》 問題③ 《直方体の体積の求め方直方体と立方体の体積の求め方を考えます。 1辺が 1 cm の立方体が何個分あるかで求めることができます。 縦×横×高さ=直方体の体積,1辺×1辺×1辺=立方体の体積となります。
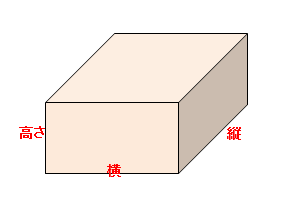
直方体の体積 ケーキ作り。 材料の分量を計算するため (レシピに載っている型と手持ちの型が違うので) 加工金属の質量を求めるのに自分の計算の答え合わせとして活用させていただきました。 リュックの容量比較で参考にさせていただきました。 直方体と立方体の体積の求め方です。 求め方は難しいものではありませんが、正確に計算できるように練習してください。 複雑な体積の求め方や単位についてもしっかり学習しましょう。 直方体の体積 直方体の体積=たて×横×高さ年 組 番 名前 524 直方体や立方体の体積 体積の求め方体積 立方体の体積の求め方 = 一辺 × 一辺 × 一辺 直方体の体積の求め方 = たて × 横 × 高さ ;
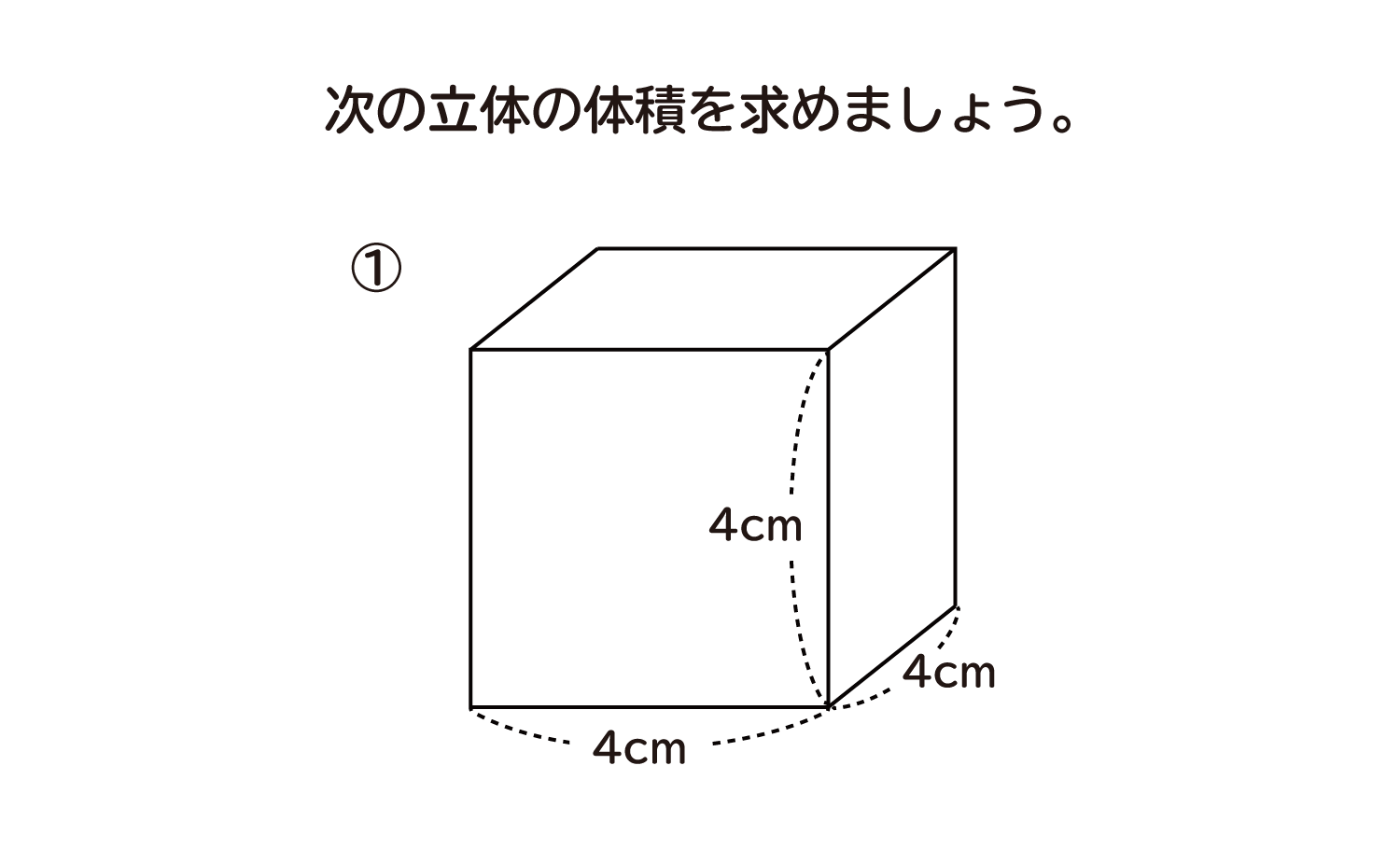
それぞれの面積はこのように計算できます。 立方体の体積: 4× 4×4=64(cm3) 4 × 4 × 4 = 64 (c m 3) 直方体の体積: 3× 4×5=60(cm3) 3 × 4 × 5 = 60 (c m 3)直方体を組み合わせた立体の体積の求め方を,求積できる形に変形して,説明することができる。 思考・判断・表現 (2)評価規準 既習の直方体や立方体の形を基に,直方体を組み合わせた立体の体積の求め方を図や式を用いて考 え,説明している。 直方体の高さの求め方を教えてください。 縦6cm、横12cmです。高さの求め方を知りたいです。 ちなみに、表面積と体積はわかりません。 こういう場合ってわかりませんよね?・直方体の高さと体積の関係を説明する。 5 本時 複合図形の体積の求め方を考える。 ・複合した立体の体積の求め




小5 直方体の体積 求め方の工夫 日本語版 Youtube




小5 複雑な立体の体積 直方体 日本語版 Youtube
体積の求め方を 考え,求めること ができる。 ・直方体を組み合わせた図形の体積の求 め方を工夫しながら多様に考える。 ・各自の考えた求め方について発表し, 検討する。 ・関どの考えも既習の直方体 や立方体の形を基にして考 えていることに気づき直方体にして考えている。 ※プロパティで子 供画面ロックを onにする。 複合図形の体積 の求め方を説明す ることができる。 ※出てこなかった 考え方は、デジタ ル教材で紹介して もよい。 まとめ (8分) ・複合図形の体積の求め方についてまとめる。5年 算数 学研教育情報資料センター 学習相談 小/算数/5年/量と測定/ 体積/理解シート 直方体の体積から,高さを求めるには,どうするの




6年算数立体の体積1 教え方




計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
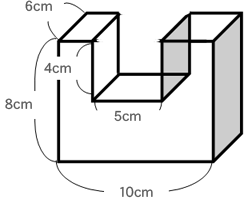
ア 角柱および円柱の体積の求め方を考えること。 直方体,立方体の場合の体積の求め方をもとにして,これらの立体の体積も計算によって求める ことができることを理解することが主なねらいとなってぼくは,直方体の一部が欠けた形とみて,大きな直方体の体積から 欠けている部分の直方体の体積をひいて求めました。 ひとし わたしは,この形を2つ組み合わせると1つの直方体になると考え, その直方体の体積の半分を求めました。 めぐみ ㋐ 3×2×3÷2問題 上の図形の体積を求めましょう。 (2)課題を設定する t:求められないと思う子,どうしてそう思う? c:デコボコしてる c:平らじゃない c:直方体じゃないから t:そうか,では今日の課題はなににしようか。 c:この図形の体積の求め方を




直方体 立方体の体積 練習 Youtube




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
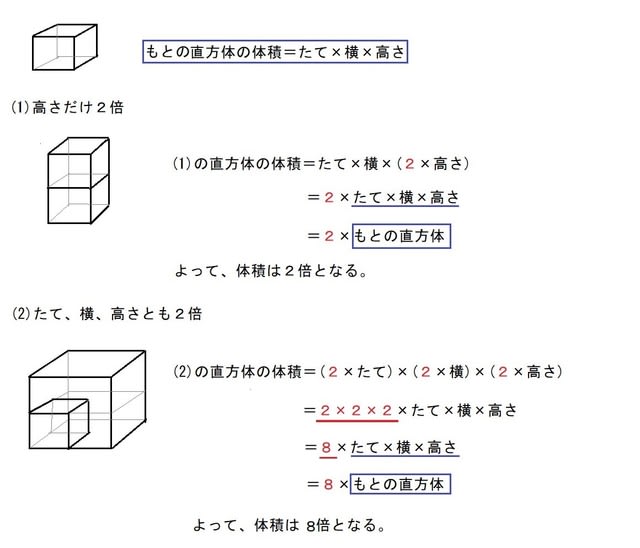
5年 学研教育情報資料センター 算数 学習相談 小/算数/5年/量と測定/ 体積/理解シート 体積 いろいろな体積の求め方基本 無料で使える学習ドリル 1 いろいろな体積の求め方 基本 目標時間 名前 右の体積を次の3つの方法で 求めましょう。 縦に2つに切って、2つの直方体に分ける。 式) 横に2つに切って、2つの直方体に分ける。 式)体積 容積の求め方 算数 教科質問直方体や立方体の体積 直方体の横の長さと体積の関係 次の図のように、直方体のたての長さと高さを変えないで、横の長さ を2倍、3倍、・・・・にすると、体積はどのように変わるか調べます。



中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
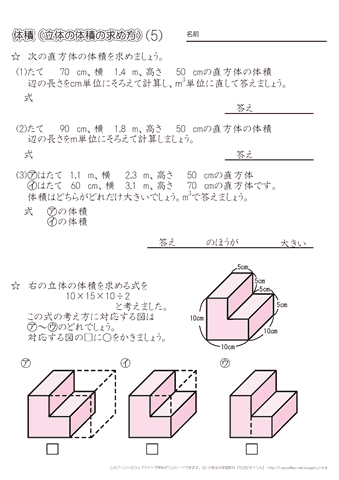
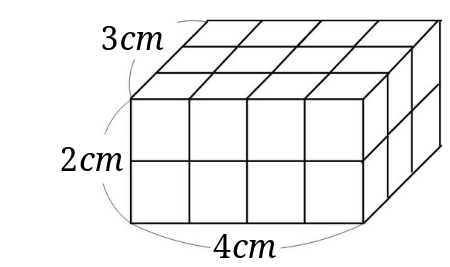
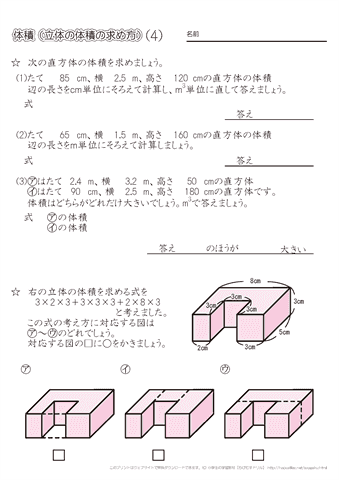
2 直方体や立方体の体積 学 年 組 氏 名 6cm 6cm 5cm 13cm cm 4cm 40cm 50cm cm 10cm 25cm 15cm 18cm =624+1=744 (答え)744cm3 1800+6300+= (例)横に補助線を引くと,奥の大きい直方体A 直方体を足すと,全体の体積が求められます。 立方体・直方体の体積の求め方|小学生に教えるための分かりやすい解説 管理人 9月 , 18 / 12月 1, 18 立体の体積という新しい分野なだけに、なかなかイメージしづらかったり、理解しづらい子は・直方体の高さと体積の関係を説明する。 5 本時 複合図形の体積の求め方を考えるCmの直方体の体積 2cmの立方体の体積 式 6 ×10×2 = mの直方体の体積 6 3 4 2 2 2 cm 3 (2)1辺の長さが 4 単位をmに直して計算し、答えはm3で求めましょう。 4 12 cmの直方体の体積 (4)たて6m、横10m、高さ2 立方体 5 個で 5 9 m3 150 0 300cmの直方体の体積 式 1 ×1




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
今日も、直方体,立方体の体積について学習をしていきます。 めあてを読んで、ワークシートに書きましょう。 めあて 直方体と立方体の体積を、計算で求める方法を考えよう。 (3)㋒の直方体の体積の求め方について考えていきます。立方体、円柱の体積と水の容量(リットル) 具体例で学ぶ数学 > 図形 > 立方体、円柱の体積と水の容量(リットル) 最終更新日 体積 1000 c m 3 = 水 1 リットル 体積 1 m 3 = 水 1000 リットル 目次 立方体の体積と水の容量 例題1 解答指導案例 画面例 体積の求め方 1:このソフトの機能とねらい 直方体の体積が「1㎝3のいくつ分」で数値化できることを提示するシミュレーション ・直方体の体積は1㎝3の立方体を敷きつめていくことにより数値化できることが視覚的に理 解できる。



立方体と直方体の体積を計算する方法とツール 具体例で学ぶ数学



体積 直方体と立方体のかさを表そう 第5学年 小学校 算数 My実践事例 日本文教出版
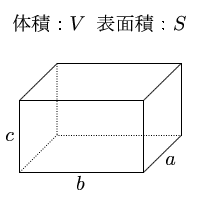
直方体の縦・横・高さを入力 縦 = 2 横 = 4 高さ = 5 直方体の体積 v = 直方体の表面積 s = 直方体の縦・横・高さを入力 縦 = 34 横 = 52 高さ = 41 直方体の体積 v = 724 直方体の表面積 s = 1050まずは、直方体を入れる前の状況を考えてみましょう。 容器に入っている水の体積は、 10cm×10cm×10cm=1000cm³ 続いて、直方体を水の中に入れてみます。 上の図の水の部分だけ取り出すと、 このように、真ん中に穴が空いた直方体になります。5年算数 体積の教え方1 子どもの学習支援by いっちに算数 体積の勉強は、体積の単位 や を理解させるとわかりやすくなります。 そのために2年「かさ」や4年「直方体と立方体」の勉強を元にして考えさせたいと思います。 忘れているお子さんには、上のリンク先でおさらいさせましょう。



1



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル
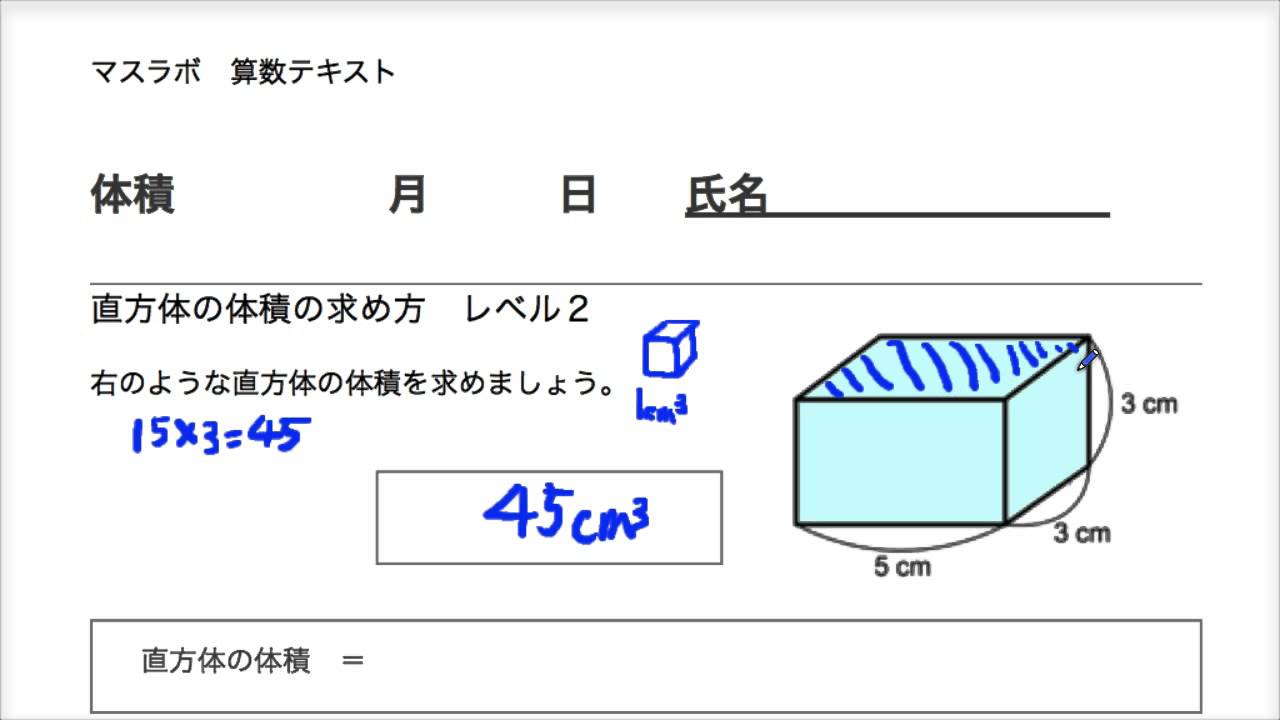
マスラボ 小学校5年 体積 レベル2 直方体の体積の求め方 Youtube 計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを立方体の体積は?1分でわかる計算、単位、公式、求め方、リットルとの関係 直方体の体積 直方体とは各面が長方形でつくられる図形です。下図に示しました。体積の公式は立方体と同じです。 よって、 直方体の体積=3×4×5=60cm 3 です。 直方体の体積〇直方体と立方体の体積の求め方を確認する。 (直方体の体積=たて×横×高さ) (立方体の体積=1辺×1辺×1辺) ★公式を記したプリントを配布する。 〇「なぜ分からないか」を問うことで,問題解決への見通しを持 たせる。




計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



直方体や立方体の体積を求める公式は どうして たて 横 高さ なの みけねこ小学校




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



5年算数体積 1 わかる教え方



直方体の表面積の求め方は 1分でわかる計算 公式と例題




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生



1



兵庫県実践事例 算数小学校6年



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー



6年算数立体の体積1 教え方



Http Www1 Iwate Ed Jp Tantou Kyouka Seika Katuyou Q Math Elementary Question Math Elementary Q 02 Pdf



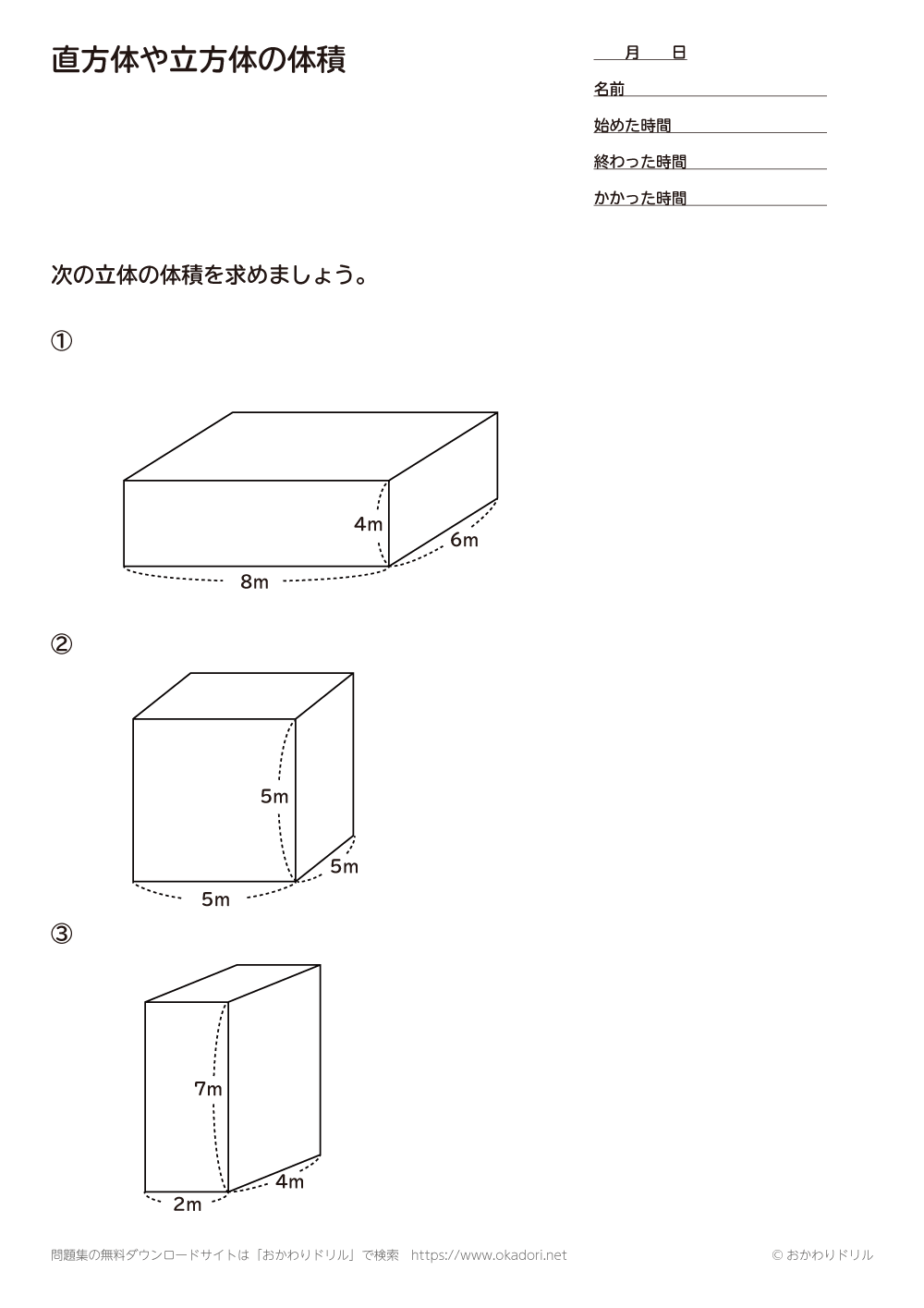
小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル




体積の求め方 計算公式一覧



立体の体積は平行線でね 基本に忠実に本質を伝える 楽天ブログ




体積 上 体積の意味から 立方体 直方体 柱 錐の体積の求め方 思考力算数練習張シリーズ 46 エム アクセス 本 通販 Amazon



直方体の体積 表面積 体積 表面積の計算 計算サイト



1




小5 算数 小5 3 直方体と立方体の体積 Youtube
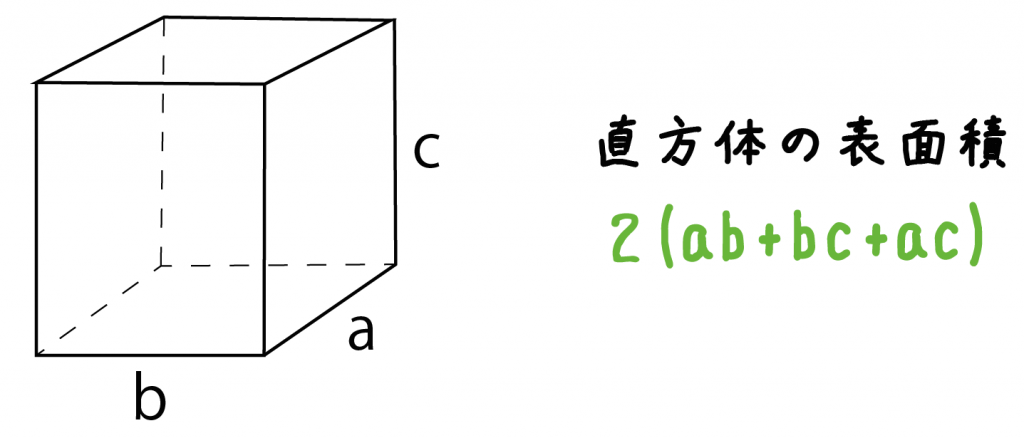



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




立体の体積を求める公式



5年算数体積2わかる教え方



直方体の体積の公式は 1分でわかる求め方 例題 直方体の面積の公式



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




直方体 立方体の体積 Youtube




超簡単 体積の求め方 苦手な数学を簡単に




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強



直方体の体積の公式は 1分でわかる求め方 例題 直方体の面積の公式



直方体を組み合わせた立方体の面積 写真参照 を解きたいのですが Yahoo 知恵袋
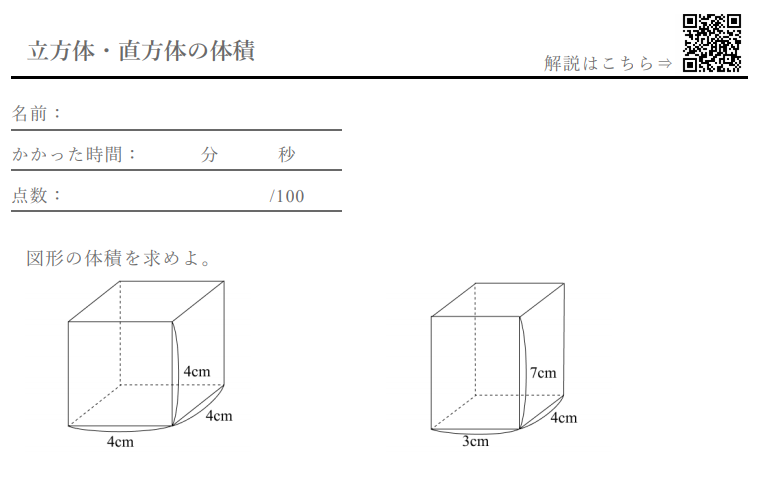



立方体 直方体 の体積 計算ドリル 問題集 数学fun



直方体 立方体の体積 小5 きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support



算数流体積の求め方 Sciencelab 冨田塾




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント




体積の求め方 計算公式一覧




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強



算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ




計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




小5 算数科 直方体の体積の求め方 Youtube




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



パワーポイント教材 那須烏山市立烏山小学校




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
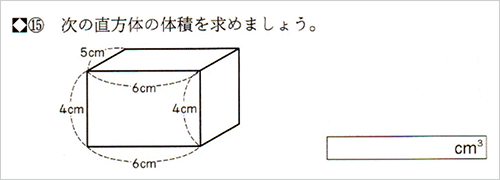



私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館



5年算数体積2わかる教え方
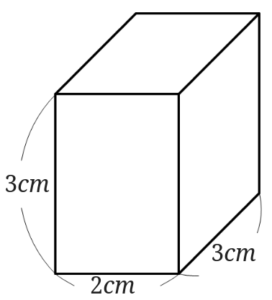



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校



直方体の体積の公式は 1分でわかる求め方 例題 直方体の面積の公式



Search Results For Page 312 横山験也のちょっと一休み




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
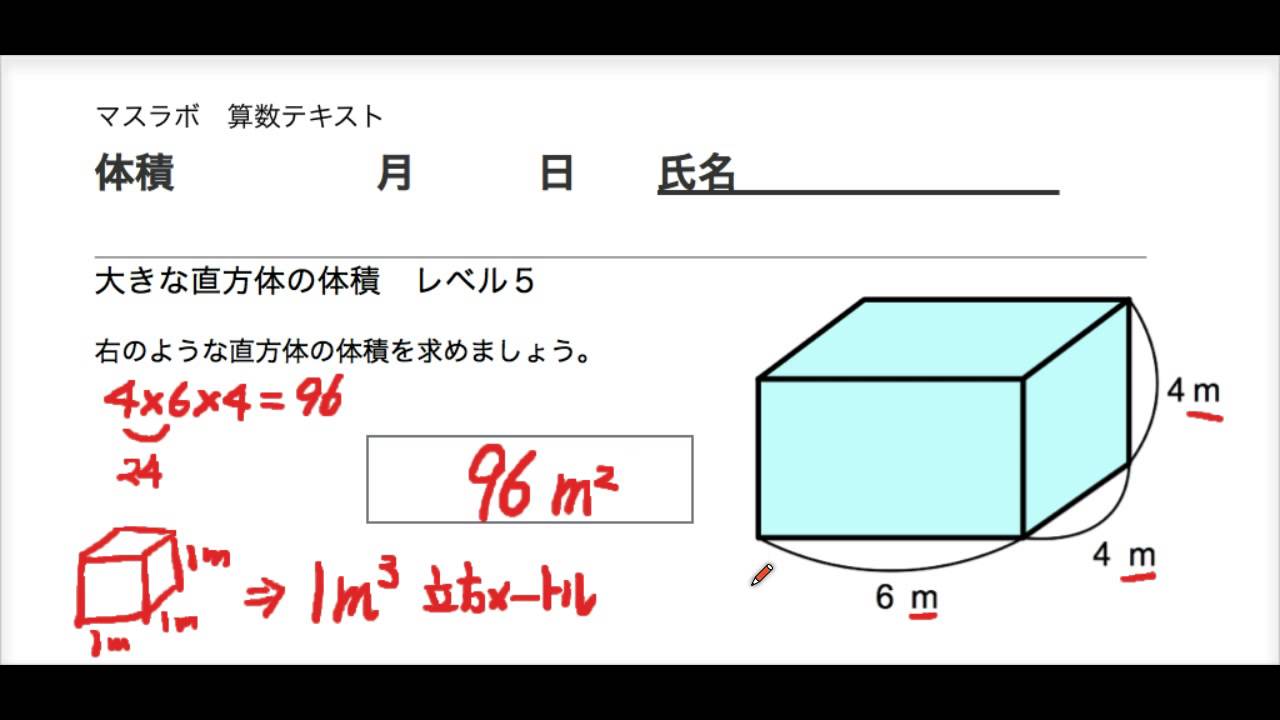



マスラボ 小学校5年 体積 レベル5 大きな直方体の体積 Youtube



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式
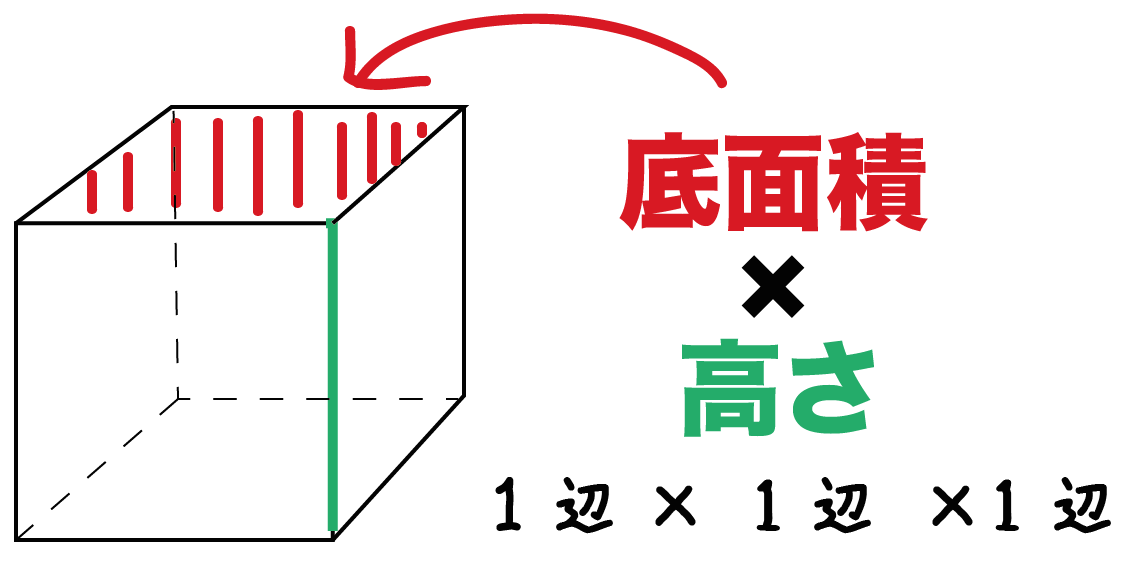



計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
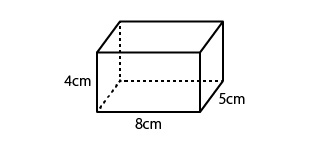



直方体の計算 もう一度やり直しの算数 数学




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




四角錐台の体積 高精度計算サイト




小5 算数 小5 5 体積の求め方のくふう Youtube




小5算数 直方体や立方体の体積の求め方がわかるかな Youtube
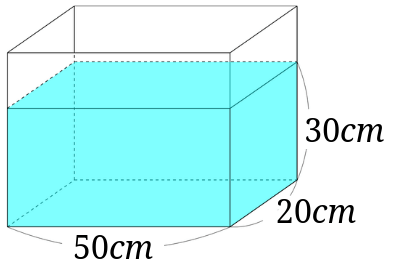



石を水の入った水槽に沈めて体積を求める問題の教え方 みけねこ小学校




多くの教師が失敗する角柱の体積の求め方 算数を究める




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧
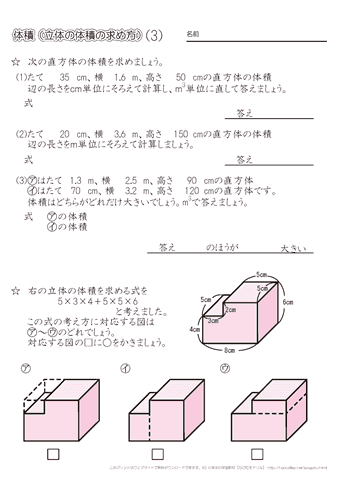



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
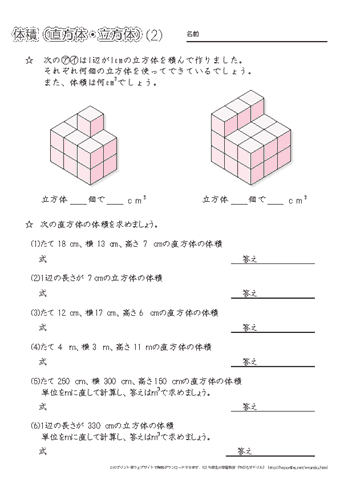



小学5年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生




小学5年生の算数 動画 直方体と立方体の体積 の問題 19ch



体積の応用



5年算数体積 1 わかる教え方



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




体積の求め方 計算公式一覧



5年算数体積 1 わかる教え方




無料印刷可能 体積 容積 求め 方




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル
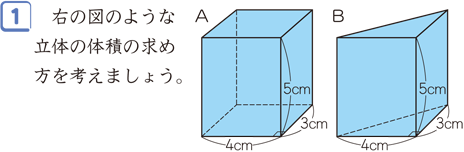



角柱と円柱の体積 算数用語集



中学生数学 この直方体の体積の求め方がわかりません 直方体の見方と体積の Yahoo 知恵袋



1
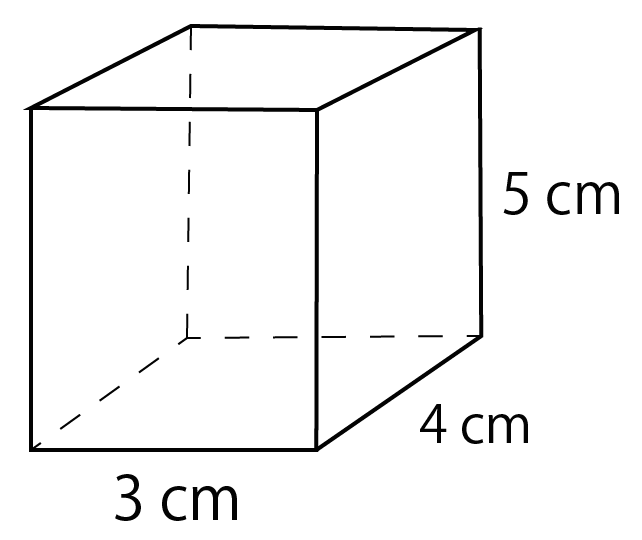



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




小学校6年生の算数 数学fun 算数 数学 小学校 算数



マスラボ 小学校5年 体積 レベル2 直方体の体積の求め方 Youtube




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強



0 件のコメント:
コメントを投稿